题目内容
17.一辆汽车开往距离出发地210千米的目的地,出发后第一小时内按原计划的速度匀速行驶,1小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求原计划的行驶速度.分析 首先设原计划的行驶速度为x千米/时,根据题意可得等量关系:原计划所用时间-实际所用时间=40分钟,根据等量关系列出方程,再解即可.
解答 解:设原计划的行驶速度为x千米/时,由题意得:
$\frac{210}{x}$-($\frac{210-x}{1.5x}$+1)=$\frac{40}{60}$,
解得:x=70,
经检验:x=70是原分式方程的解.
答:原计划的行驶速度为70千米/时.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,表示出原计划所用时间和实际所用时间,根据时间关系列出分式方程.

练习册系列答案
相关题目
5.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
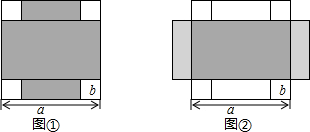

| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
12.将抛物线y=x2+5向右平移1个单位长度,再向下平移2个单位长度,后,得到的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
 如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分.
如图,在?ABCD中,AE⊥BD于点E,CF⊥BD于点F,G、H分别为AD、BC的中点.求证:EF、GH互相平分. 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.