题目内容
14.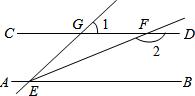 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )| A. | 130° | B. | 140° | C. | 150° | D. | 160° |
分析 根据平行线的性质可得∠GEB=∠1=60°,然后根据EF为∠GEB的平分线可得出∠FEB的度数,根据两直线平行,同旁内角互补即可得出∠2的度数.
解答 解:∵AB∥CD,
∴∠GEB=∠1=60°,
∵EF为∠GEB的平分线,
∴∠FEB=$\frac{1}{2}$∠GEB=30°,
∴∠2=180°-∠FEB=150°.
故选C.
点评 本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
5. 如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
 如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
2.一组数据从小到大排列为2,3,4,x,6,9.这组数据的中位数是5,那么这组数据的众数为( )
| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
9.一个正多边形内角和等于540°,则这个正多边形的每一个外角等于( )
| A. | 72° | B. | 60° | C. | 108° | D. | 90°. |
19.若一个正多边形的一个内角是140°,则这个多边形是( )
| A. | 正七边形 | B. | 正八边形 | C. | 正九边形 | D. | 正十边形 |
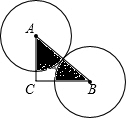 如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( ) 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则sin∠ABC=$\frac{\sqrt{5}}{5}$.
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则sin∠ABC=$\frac{\sqrt{5}}{5}$.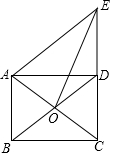 如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.