题目内容
1. 如图所示,在△ABC中,BD,CD分别为∠ABC,∠ACB外角平分线,则∠D与∠A有什么关系,并说明理由.
如图所示,在△ABC中,BD,CD分别为∠ABC,∠ACB外角平分线,则∠D与∠A有什么关系,并说明理由.
分析 根据三角形的内角和定理,可得∠A+∠B+∠C=180°,∠D+$\frac{1}{2}$(180°-∠B)+$\frac{1}{2}$(180°-∠C)=180°,据此判断出∠D与∠A有什么关系即可.
解答 解:根据三角形的内角和定理,可得
∠A+∠B+∠C=180°…(1),
∠D+$\frac{1}{2}$(180°-∠B)+$\frac{1}{2}$(180°-∠C)=180°…(2),
由(2),可得
∠D=$\frac{1}{2}$∠B+$\frac{1}{2}$∠C…(3),
由(1)(3),可得
∠D+2∠A=180°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质以及应用,要熟练掌握.

练习册系列答案
相关题目
3.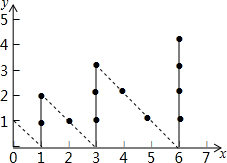 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )| A. | 886 | B. | 903 | C. | 946 | D. | 990 |
7.下列方程中是一元二次方程的是( )
| A. | (x-1)(3+x)=5 | B. | x2+$\frac{1}{x}$-$\frac{9}{2}$=0 | C. | y2+2x+4=0 | D. | 4x2=(2x-1)2 |
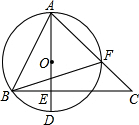 变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?
变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?