题目内容
已知点A的坐标是(0,4),点B的坐标是(-4,2),那么过A、B两点的直线表达式为 .
考点:待定系数法求一次函数解析式
专题:计算题
分析:设一次函数解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出解析式.
解答:解:设一次函数解析式为y=kx+b,
把A(0,4),B(-4,2)代入得:
,
解得:k=
,b=4,
则一次函数解析式为y=
x+4.
故答案为:y=
x+4.
把A(0,4),B(-4,2)代入得:
|
解得:k=
| 1 |
| 2 |
则一次函数解析式为y=
| 1 |
| 2 |
故答案为:y=
| 1 |
| 2 |
点评:此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列性质正方形具有而矩形不具有的是( )
| A、四角相等 |
| B、对角线互相垂直 |
| C、对角线相等 |
| D、对角线互相平分 |
已知x2+y2=13,xy=-2,则①(x-y)2=17;②(x+y)2-(x-y)2=8;③x+y=3;④(2x-y)(2y-x)=-36,其中正确的有( )
| A、1 个 |
| B、2 个 |
| C、3 个 |
| D、4 个 |
 如图,AB∥DE,若∠B=30°,∠D=140°,则∠C的大小是
如图,AB∥DE,若∠B=30°,∠D=140°,则∠C的大小是 二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
二次函数y=x2+bx+c的图象经过点(4,3),(3,0).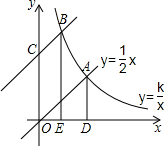 如图,直线y=
如图,直线y= 解一元一次不等式及不等式组,并把它的解集在数轴上分别表示出来.
解一元一次不等式及不等式组,并把它的解集在数轴上分别表示出来.