题目内容
4.方程x2-$\frac{10}{x}$+1=-4x的正数根的取值范围是( )| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
分析 方程可以化成y1=x2+4x+1和y2=$\frac{10}{x}$图象在第一象限内的交点问题,然后结合图象即可求解.
解答 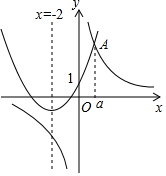 解:方程x2-$\frac{10}{x}$+1=-4x即x2+4x+1=$\frac{10}{x}$.
解:方程x2-$\frac{10}{x}$+1=-4x即x2+4x+1=$\frac{10}{x}$.
函数y1=x2+4x+1和y2=$\frac{10}{x}$的大体图象是:
当x=1时,y1=x2+4x+1=6,y2=$\frac{10}{x}$=10,此时y1<y2,即1<a,
当x=2时,y1=4+8+1=13,y2=5,此时y1>y2,则a>2,
则a在1与2之间,即1<a<2.
即方程x2-$\frac{10}{x}$+1=-4x的正数根的取值范围是1<x<2.
故选B.
点评 本题考查了二次函数与反比例函数图象的交点问题,理解方程的解就是函数图象的交点的横坐标是关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
14.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | 2a-a=2 | C. | a2+a2=a4 | D. | (a2)3=a5 |
9.抽查的甲、乙两班部分学生的视力,记录如下:
(1)求两组数据的平均数,众数,中位数.
(2)比较两组数据的特征,谈谈对“极端值”的认识.
| 甲班 | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| 乙班 | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
(2)比较两组数据的特征,谈谈对“极端值”的认识.
11.定义新运算:对于任意实数m、n都有m☆n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:-3☆2=(-3)2×2+2=20.根据以上知识解决问题:若2☆a的值小于0,请判断方程:2x2-bx+a=0的根的情况( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
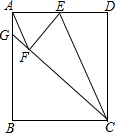 如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.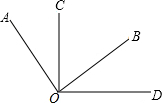 如图,∠AOB=∠COD=90°
如图,∠AOB=∠COD=90°