题目内容
13.如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为2$\sqrt{3}$,当∠DOE=15°时,求线段EF的长;
(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,证明:PE=2PF.
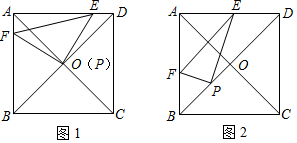
分析 (1)①根据正方形的性质和旋转的性质即可证得:△AOF≌△DOE根据全等三角形的性质证明;
②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;
(2)首先过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系.
解答 (1)①证明:∵四边形ABCD是正方形,
∴OA=OD,∠OAF=∠ODE=45°,∠AOD=90°,
∴∠AOE+∠DOE=90°,
∵∠EPF=90°,
∴∠AOF+∠AOE=90°,
∴∠DOE=∠AOF,
在△AOF和△DOE中,
$\left\{\begin{array}{l}{∠OAF=∠ODE}\\{OA=OD}\\{∠AOF=∠DOE}\end{array}\right.$,
∴△AOF≌△DOE,
∴AF=DE;
②解:过点O作OG⊥AB于G,
∵正方形的边长为2$\sqrt{3}$,
∴OG=$\frac{1}{2}$BC=$\sqrt{3}$,
∵∠DOE=15°,△AOF≌△DOE,
∴∠AOF=15°,
∴∠FOG=45°-15°=30°,
∴OF=$\frac{OG}{cos∠DOG}$=2,
∴EF=$\sqrt{O{F}^{2}+O{E}^{2}}$=2$\sqrt{2}$;
(2)证明:如图2,过点P作HP⊥BD交AB于点H,
则△HPB为等腰直角三角形,∠HPD=90°,
∴HP=BP,
∵BD=3BP,
∴PD=2BP,
∴PD=2HP,
又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,
∴∠HPF=∠DPE,
又∵∠BHP=∠EDP=45°,
∴△PHF∽△PDE,
∴$\frac{PF}{PE}$=$\frac{PH}{PD}$=$\frac{1}{2}$,
∴PE=2PF.
点评 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.

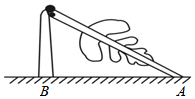 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )| A. | 10m | B. | 15m | C. | 18m | D. | 20m |
| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
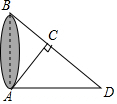 如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )| A. | 30米 | B. | 35米 | C. | 40米 | D. | 45米 |
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
 如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$.
如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$. 如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.
如图,已知抛物线y=ax2+bx(a≠0)经过A(4,4)、B(2,-2)两点,与x轴交于点C.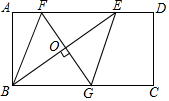 如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.