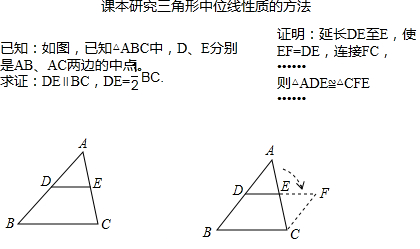
题目内容
11.定义新运算:对于任意实数m、n都有m☆n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:-3☆2=(-3)2×2+2=20.根据以上知识解决问题:若2☆a的值小于0,请判断方程:2x2-bx+a=0的根的情况( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
分析 先利用新定义得到22•a+a<0,解得a<0,再计算判别式,利用a的范围可判断△>0,从而可判断方程根的情况.
解答 解:∵2☆a的值小于0,
∴22•a+a<0,解得a<0,
∴△=b2-4×2×a>0,
∴方程有两个不相等的两个实数根.
故选B.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
4.方程x2-$\frac{10}{x}$+1=-4x的正数根的取值范围是( )
| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
2.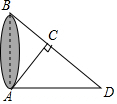 如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
 如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )
如图所示,为了测量出A、B两点间的距离,在地面上找到一点C,连接AC、BC,使得∠ACB=90°,然后在BC的延长线上确定点D,使得CD=CB.现已知AD的长是一元一次方程$\frac{x-7}{2}$+$\frac{x+4}{7}$=26的解,则A、B两点间的距离为( )| A. | 30米 | B. | 35米 | C. | 40米 | D. | 45米 |
20.-|-2017|的相反数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
1. 在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
 在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:$\sqrt{2}$ |