题目内容
在圆外切四边形ABCD中,AB:BC:CD:AD只可能是( )
| A、2:3:4:5 |
| B、3:4:6:5 |
| C、5:4:1:3 |
| D、3:4:2:5 |
考点:切线长定理
专题:
分析:根据圆外切四边形的对边和相等逐个判断即可.
解答:解:∵四边形ABCD是圆外切四边形,
∴AB+CD=AD+BC,
A、2+4≠3+5,故本选项错误;
B、3+6=4+5,故本选项正确;
C、5+1≠4+3,故本选项错误;
D、3+2≠4+5,故本选项错误;
故选B.
∴AB+CD=AD+BC,
A、2+4≠3+5,故本选项错误;
B、3+6=4+5,故本选项正确;
C、5+1≠4+3,故本选项错误;
D、3+2≠4+5,故本选项错误;
故选B.
点评:本题考查了圆外切四边形和切线长定理的应用,题目比较好,难度不是很大.

练习册系列答案
相关题目
已知点M在线段AB上,在①AB=2AM、②BM=
AB、③AM=BM、④AM+BM=AB四个式子中,能说明M是AB的中点的式子是( )
| 1 |
| 2 |
| A、①③④ | B、①②③ |
| C、①②④ | D、①②③④ |
已知二次函数y=mx2+(2m-1)x+m的图象与x轴有两个交点,则m的取值范围是( )
A、m<
| ||
B、m≤
| ||
C、m<
| ||
D、m≤
|
下列说法,正确的是( )
| A、若|a|=-a,则a<0 | ||||
| B、若|a|=|b|=2,则a=2,b=±2 | ||||
C、若a=b,m为有理数,则
| ||||
| D、若a<0,b>0,则ab<0 |
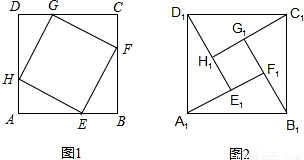 在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于
在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于 如图,AB是⊙O的直径,∠C=40°,则∠ABD=
如图,AB是⊙O的直径,∠C=40°,则∠ABD= 如图,在?ABCD中,AE⊥BD,CF⊥BD,求证:BF=DE.
如图,在?ABCD中,AE⊥BD,CF⊥BD,求证:BF=DE.