题目内容
已知二次函数y=mx2+(2m-1)x+m的图象与x轴有两个交点,则m的取值范围是( )
A、m<
| ||
B、m≤
| ||
C、m<
| ||
D、m≤
|
考点:抛物线与x轴的交点
专题:
分析:由二次函数图象与x轴有两个不同交点化为方程有两个不同的解.
解答:解:∵二次函数图象y=y=mx2+(2m-1)x+m与x轴有两个不同交点,
∴m≠0,△=(2m-1)2-4m2>0.
整理,得
-4m+1>0,
解得解得,m<
,且m≠0.
故选:C.
∴m≠0,△=(2m-1)2-4m2>0.
整理,得
-4m+1>0,
解得解得,m<
| 1 |
| 4 |
故选:C.
点评:本题考查了抛物线与x轴的交点.注意二次函数与二次方程的关系,属于基础题.

练习册系列答案
相关题目
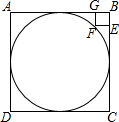 圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )
圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )A、4+2
| ||
| B、2π | ||
C、5
| ||
D、
| ||
E、4
|
在圆外切四边形ABCD中,AB:BC:CD:AD只可能是( )
| A、2:3:4:5 |
| B、3:4:6:5 |
| C、5:4:1:3 |
| D、3:4:2:5 |
 如图,是由7块正方体木块堆成的物体,分别画出从正面、左面、上面看的平面图形.
如图,是由7块正方体木块堆成的物体,分别画出从正面、左面、上面看的平面图形.