题目内容
7.解三元一次方程组$\left\{\begin{array}{l}{z=x+y,①}\\{3x-2y-2z=-5,②}\\{2x+y-z=3,③}\end{array}\right.$.分析 先把①分别代入②③后消去z,再解二元一次方程组即可.
解答 解:$\left\{\begin{array}{l}{z=x+y,①}\\{3x-2y-2z=-5,②}\\{2x+y-z=3,③}\end{array}\right.$,
把①代入②得:x-4y=-5④,
把①代入③得:x=3,
把x=3代入④得:y=2,
把x=3,y=2代入①得:z=5,
所以方程组的解是:$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=5}\end{array}\right.$
点评 本题考查了解三元一次方程组,解题的关键是掌握消元思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.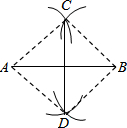 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 等腰梯形 |
16.x,y的方程组$\left\{\begin{array}{l}{x+y=2a+7}\\{x-2y=4a-3}\end{array}\right.$的解为正数,且x的值小于y的值,求a的取值范围.
17.$\frac{1}{2}$的相反数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | 0.5 | D. | 一2 |
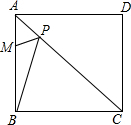 已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.
已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.