题目内容
16.x,y的方程组$\left\{\begin{array}{l}{x+y=2a+7}\\{x-2y=4a-3}\end{array}\right.$的解为正数,且x的值小于y的值,求a的取值范围.分析 把a当作已知数,解方程组求出方程组的解(x y的值),根据已知得出不等式组,求出a的取值范围即可.
解答 解:方程组$\left\{\begin{array}{l}{x+y=2a+7}\\{x-2y=4a-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{8a+11}{3}}\\{y=\frac{-2a+10}{3}}\end{array}\right.$,
∵方程组的解为正数,且x的值小于y的值,
∴$\left\{\begin{array}{l}{\frac{8a+11}{3}>0}\\{\frac{-2a+10}{3}>0}\\{\frac{8a+11}{3}<\frac{-2a+10}{3}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a>-\frac{11}{8}}\\{a<5}\\{a<-\frac{1}{10}}\end{array}\right.$
∴$-\frac{11}{8}<a<-\frac{1}{10}$.
点评 本题综合考查了解方程组和解不等式组的应用,关键是根据题意求出关于a的不等式组.

练习册系列答案
相关题目
5.已知等腰三角形的腰长为2,底边长不可能的是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.下列方程有实数根的有( )
①x2+x+4=0;②x2+4x+4=0;③x2+4x-2=0.
①x2+x+4=0;②x2+4x+4=0;③x2+4x-2=0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
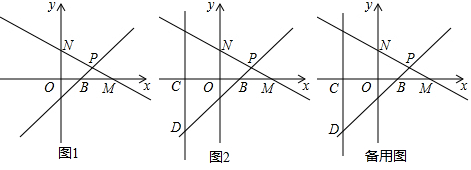
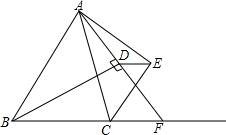 已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.
已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.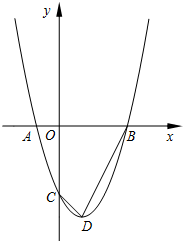 如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.