题目内容
12．解方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{3}-\frac{z}{4}=3}\\{\frac{x}{2}+\frac{y}{3}-z=4}\\{\frac{x}{3}-\frac{y}{2}+\frac{z}{2}=3}\end{array}\right.$．分析 先把原方程组化简后，再①+③和②+③×2消去z后，解二元一次方程组即可．
解答 解：原方程组化简为：$\left\{\begin{array}{l}{6x-4y-3z=36①}\\{3x+2y-6z=24②}\\{2x-3y+3z=18③}\end{array}\right.$，
①+③得：8x-7y=54④，
②+③×2得：7x-4y=60⑤，
⑤×7-④×4得：x=12，
把x=12代入④得：y=6，
把x=12，y=6代入③得：z=4，
所以方程组的解是：$\left\{\begin{array}{l}{x=12}\\{y=6}\\{z=4}\end{array}\right.$
点评 本题考查了解三元一次方程组，解题的关键是掌握消元思想．
练习册系列答案
备战中考寒假系列答案
相关题目
18．
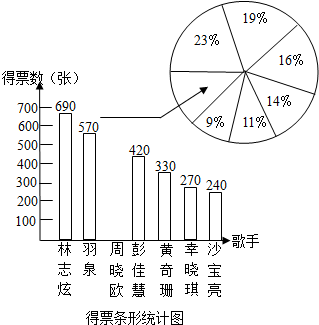今年初湖南台“我是歌手”栏目受到广泛关注，某期比赛结果统计如下，并制作成统计图，请根据下列统计情况，回答下列问题．
（1）请补全条形统计图，并计算出沙宝亮的得票率；
（2）请计算出“沙宝亮的得票率”在扇形图中对应的圆心角的度数；
（3）在这场比赛中小丽觉得“林志炫、彭佳慧、周晓欧、黄奇珊”这四个人唱的都很好，她都想投票给他们，但比赛规定，每张选票只能选三个人，（排名不分先后）小丽最后的选票恰好是“林志炫、周晓欧、黄奇珊”的概率是多少？（请画出树状图或列表说明）
今年初湖南台“我是歌手”栏目受到广泛关注，某期比赛结果统计如下，并制作成统计图，请根据下列统计情况，回答下列问题．| 歌手 | 得票数（张） | 得票率 |
| 林志炫 | 690 | 23% |
| 羽泉 | 570 | 19% |
| 周晓欧 | 480 | 16% |
| 彭佳慧 | 420 | 14% |
| 黄奇珊 | 330 | 11% |
| 幸晓琪 | 270 | 9% |
| 沙宝亮 | 240 | |
| 合计 | 3000 | 100% |
（2）请计算出“沙宝亮的得票率”在扇形图中对应的圆心角的度数；
（3）在这场比赛中小丽觉得“林志炫、彭佳慧、周晓欧、黄奇珊”这四个人唱的都很好，她都想投票给他们，但比赛规定，每张选票只能选三个人，（排名不分先后）小丽最后的选票恰好是“林志炫、周晓欧、黄奇珊”的概率是多少？（请画出树状图或列表说明）
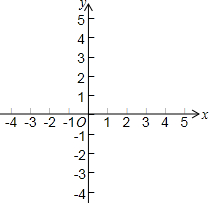利用函数图象解方程组$\left\{\begin{array}{l}{3x+2y=5}\\{2x-y=1}\end{array}\right.$．