题目内容
 如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为
如图,已知坐标平面内有两点A(1,0),B(-2,4),现将AB绕着点A顺时针旋转90°至AC位置,则点C的坐标为考点:坐标与图形变化-旋转
专题:几何变换
分析:作BD⊥x轴于D,CE⊥x轴于E,由A(1,0),B(-2,4)得到AD=3,BD=4,根据旋转的性质得∠BAC=90°,AB=AC,再利用等角的余角相等得∠B=∠CAE,则可证明△ABD≌△CAE,所以AE=BD=4,CE=AD=3,OE=OA+AE=5,然后根据第一象限点的坐标特征写出C点坐标.
解答: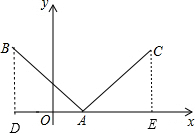 解:作BD⊥x轴于D,CE⊥x轴于E,如图,
解:作BD⊥x轴于D,CE⊥x轴于E,如图,
∵A(1,0),B(-2,4),
∴AD=3,BD=4,
∵AB绕着点A顺时针旋转90°至AC位置,
∴∠BAC=90°,AB=AC,
∴∠BAD+∠CAE=90°,
而∠BAD+∠B=90°,
∴∠B=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AE=BD=4,CE=AD=3,
∴OE=OA+AE=5,
∴C点坐标为(5,3).
故答案为(5,3).
 解:作BD⊥x轴于D,CE⊥x轴于E,如图,
解:作BD⊥x轴于D,CE⊥x轴于E,如图,∵A(1,0),B(-2,4),
∴AD=3,BD=4,
∵AB绕着点A顺时针旋转90°至AC位置,
∴∠BAC=90°,AB=AC,
∴∠BAD+∠CAE=90°,
而∠BAD+∠B=90°,
∴∠B=∠CAE,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AE=BD=4,CE=AD=3,
∴OE=OA+AE=5,
∴C点坐标为(5,3).
故答案为(5,3).
点评:本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=3,BE=4,则阴影部分的面积是( )
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=3,BE=4,则阴影部分的面积是( )| A、19 | B、15 | C、12 | D、6 |
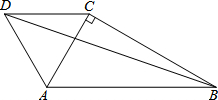 如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2
如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2 已知:如图,在Rt△ABC中,∠A=90°,AB=AC=1,P是AB边上不与A点、B点重合的任意一个动点,PQ⊥BC于点Q,QR⊥AC于点R.
已知:如图,在Rt△ABC中,∠A=90°,AB=AC=1,P是AB边上不与A点、B点重合的任意一个动点,PQ⊥BC于点Q,QR⊥AC于点R.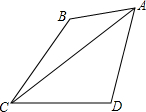 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.