题目内容
2. 甲、乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图象如图所示,且甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
甲、乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图象如图所示,且甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:(1)求乙的速度?
(2)甲中途停止了多长时间?
(3)两人相遇时,离B地的路程是多少千米?
分析 (1)根据图象可知,乙1.5小时行走20千米,根据速度=路程÷时间即可求出乙的速度;
(2)先由甲0.5小时行走8千米求出甲原来的速度,由(2.5-a)小时行走(20-8)千米表示出甲后来的速度,根据甲停止一段时间后再次行走的速度是原来的一半列出关于a的方程,求出a的值,进而求解即可;
(3)先求出两人相遇时乙行走的路程,再用A、B两地之间的距离减去乙行走的路程即可.
解答 解:(1)根据图象,可得乙的速度为:$\frac{20}{2-0.5}$=$\frac{40}{3}$(km/h);
(2)甲原来的速度为:$\frac{8}{0.5}$=16(km/h),
甲后来的速度为:$\frac{20-8}{2.5-a}$(km/h),
由题意,得$\frac{20-8}{2.5-a}$=$\frac{1}{2}$×16,
解得a=1,
则a-0.5=1-0.5=0.5.
故甲中途停止了0.5小时;
(3)(1-0.5)×$\frac{40}{3}$=$\frac{1}{2}$×$\frac{40}{3}$=$\frac{20}{3}$(km),
(8-$\frac{20}{3}$)÷($\frac{40}{3}$-8)
=$\frac{4}{3}$÷$\frac{16}{3}$
=$\frac{1}{4}$(h),
乙离A地的路程为:$\frac{40}{3}$×($\frac{1}{2}$+$\frac{1}{4}$)=10(km),
他们离B地的路程是20-10=10(km).
点评 本题考查了函数的图象,路程、速度与时间关系的应用,学会观察函数图象,从函数图象中获取有用信息是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.探索规律,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形有5n+3个,周长为10n+8.
(3)写出第30个图形的周长.

(1)观察图形,填写下表:
| 图形个数( n ) | (1) | (2) | (3) |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
(3)写出第30个图形的周长.
 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.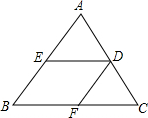 如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)
如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号) 如图:一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分)余下部分进行了绿化,若已知绿化面积为540m2,求道路的宽.
如图:一长为32m、宽为20m的矩形地面上修建有同样宽的道路(图中阴影部分)余下部分进行了绿化,若已知绿化面积为540m2,求道路的宽. 某开发区有一块三角形的空地BCD,计划在该空地上种草皮,∠A=60°,AB=AD=8m,CD=10m,BC=6m,若每平方米草皮需要200元,问需要投入多少资金?($\sqrt{3}$≈1.73)
某开发区有一块三角形的空地BCD,计划在该空地上种草皮,∠A=60°,AB=AD=8m,CD=10m,BC=6m,若每平方米草皮需要200元,问需要投入多少资金?($\sqrt{3}$≈1.73)