题目内容
15.(1)因式分解:①2x3-18x;
②(x2+2x)2+2(x2+2x)+1
③先因式分解,再求值:已知a+b=2,ab=2,求$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3的值.
(2)先化简,再求值:($\frac{3x}{x-1}$-$\frac{2x}{x+1}$)•$\frac{{x}^{2}-1}{x}$,其中x=$\sqrt{5}$-5.
分析 (1)①提公因式后再利用平方差公式分解因式;
②利用了两次完全平方公式进行因式分解;
③提公因式$\frac{1}{2}$ab后,再利用完全平方公式进行因式分解;
(2)先利用乘法分配律去括号,约分后,再去括号,代入求值即可.
解答 解:(1)①2x3-18x=2x(x2-9)=2x(x+3)(x-3);
②(x2+2x)2+2(x2+2x)+1,
=(x2+2x+1)2,
=(x+1)4;
③$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3,
=$\frac{1}{2}$ab(a2+2ab+b2),
=$\frac{1}{2}$ab(a+b)2,
当a+b=2,ab=2时,原式=$\frac{1}{2}$×2×22=4;
(2)($\frac{3x}{x-1}$-$\frac{2x}{x+1}$)•$\frac{{x}^{2}-1}{x}$,
=$\frac{3x}{x-1}$•$\frac{(x+1)(x-1)}{x}$-$\frac{2x}{x+1}$$•\frac{(x+1)(x-1)}{x}$,
=3(x+1)-2(x-1),
=x+5,
当x=$\sqrt{5}$-5时,原式=$\sqrt{5}$-5+5=$\sqrt{5}$.
③$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3
点评 本题既考查出因式分解及应用,又考查了分式的化简求值,计算量不大,但要细心完成;做好本题的关键是熟练掌握完全平方公式和平方差公式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10.探索规律,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形有5n+3个,周长为10n+8.
(3)写出第30个图形的周长.

(1)观察图形,填写下表:
| 图形个数( n ) | (1) | (2) | (3) |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
(3)写出第30个图形的周长.
20.如果每盒笔有18支,售价12元,用y(元)表示笔的售价,x表示笔的支数,那么y与x之间的关系式应该是( )
| A. | y=12x | B. | y=18x | C. | y=$\frac{2}{3}$x | D. | y=$\frac{3}{2}x$ |
 阅读理解下面内容,并解决问题:
阅读理解下面内容,并解决问题: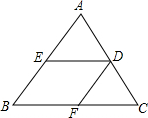 如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)
如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号) 如图,某小区有A、B、C、D四栋楼,现在要建造一个水塔P,请画出水塔P应建在何位置,才能使它到四栋楼的距离之和最小,说明画图的原理.
如图,某小区有A、B、C、D四栋楼,现在要建造一个水塔P,请画出水塔P应建在何位置,才能使它到四栋楼的距离之和最小,说明画图的原理. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画出的两条直线之所以平行,其原理是同位角相等,两直线平行.
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画出的两条直线之所以平行,其原理是同位角相等,两直线平行.