题目内容
17.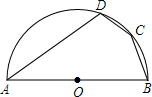 已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.
已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.
分析 首先连接BD,OC,相交于点E,由DC=BC,可得OC⊥BD,然后设OE=x,由BE2=OB2-OE2=BC2-CE2,可得方程22-x2=12-(2-x)2,解此方程即可求得OE的长,然后由三角形中位线的性质,求得答案.
解答 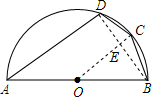 解:连接BD,OC,相交于点E,
解:连接BD,OC,相交于点E,
∵DC=BC,
∴$\widehat{CD}$=$\widehat{BC}$,
∴OC⊥BD,BE=DE,
∵DC=BC=$\frac{1}{4}$AB=1,
∴AB=4,
∴OC=OB=2,
设OE=x,则CE=OC-OE=2-x,
∵BE2=OB2-OE2=BC2-CE2,
∴22-x2=12-(2-x)2,
解得:x=$\frac{7}{4}$,
∵OA=OB,
∴AD=2OE=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 此题考查了垂径定理、三角形中位线的性质以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
12.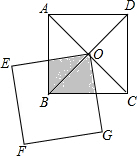 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 始终不变 | D. | 先由大变小,然后又由小变大 |
2.某技能培训学校对120名学员的操作技能进行了考核,并随机抽取了30名学员的成绩,统计结果如表所示:
(Ⅰ)求本次随机抽取的样本数据的平均数、众数和中位数;
(Ⅱ)从全部获得100分的学员中随机选派2人参加全市的操作技能大赛,小明的成绩恰好是100分,估计小明被选中的概率是多少?
| 分数 | 100 | 95 | 90 | 85 | 80 | 75 |
| 人数 | 2 | 6 | 10 | 4 | 6 | 2 |
(Ⅱ)从全部获得100分的学员中随机选派2人参加全市的操作技能大赛,小明的成绩恰好是100分,估计小明被选中的概率是多少?
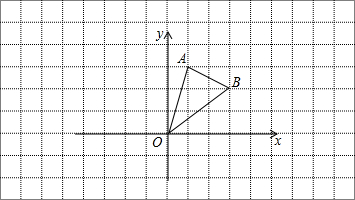
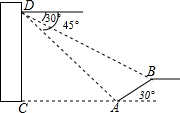 如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).
如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).