题目内容
6.(1)计算:(-$\frac{1}{3}$)-2-16÷(-2)3+(π-tan60°)0-2$\sqrt{3}$cos30°(2)解方程:$\frac{2}{{x}^{2}-4}$-$\frac{x}{2-x}$=1.
分析 (1)原式利用零指数幂、负整数指数幂法则,乘方的意义,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=9+2+1-3=9;
(2)去分母得:2+x2+2x=x2-4,
解得:x=-3,
经检验x=-3是分式方程的解.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
| A. | 小明的影子比小强的影子长 | B. | 小明的影子比小强的影子短 | ||
| C. | 小明的影子和小强的影子一样长 | D. | 两人的影子长度不确定 |
11.在实数-2,0,3,$\sqrt{3}$中,最大的实数是( )
| A. | -2 | B. | 0 | C. | 3 | D. | $\sqrt{3}$ |
18.解方程:
(1)-5x+5=-6x;
(2)$4x-\frac{1}{2}x=3+4$;
(3)$\frac{2}{5}x-4=12+\frac{3}{5}x$;
(4)2-3.5x=4.5x-1.
(1)-5x+5=-6x;
(2)$4x-\frac{1}{2}x=3+4$;
(3)$\frac{2}{5}x-4=12+\frac{3}{5}x$;
(4)2-3.5x=4.5x-1.
16.已知三条线段a>b>c>0,则它们能组成三角形的条件是( )
| A. | a=b+c | B. | a+c>b | C. | b-c>a | D. | a<b+c |
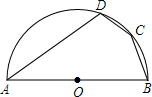 已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.
已知,如图所示,C,D是以AB为直径的半圆O上的两点,且DC=BC=$\frac{1}{4}$AB=1.求AD的长.