题目内容
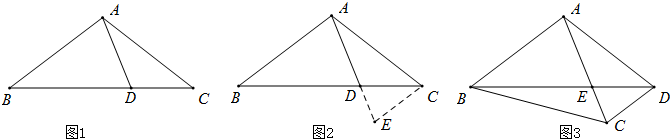
已知：如图，在△ABC中，F是AB上一点，E是CD上一点，BE⊥DF于G，∠1=∠C，∠2+∠D=90°，试说明AB∥CD．考点：平行线的判定与性质
专题：证明题
分析：由已知角相等，利用同位角相等两直线平行得到BE与FC平行，根据DF垂直与BE，得到DF垂直于FC，得到∠2与∠BFD互余，根据∠2与∠D互余，利用同角的余角相等得到一对内错角相等，利用内错角相等两直线平行即可得证．
解答：证明：∵∠1=∠C，
∴BE∥CF，
∵DF⊥BE，
∴DF⊥CF，
∴∠CFD=90°，
∴∠2+∠BFD=90°，
∵∠2+∠D=90°，
∴∠D=∠BFD，
∴AB∥CD．
∴BE∥CF，
∵DF⊥BE，
∴DF⊥CF，
∴∠CFD=90°，
∴∠2+∠BFD=90°，
∵∠2+∠D=90°，
∴∠D=∠BFD，
∴AB∥CD．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
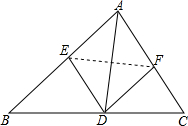如图，在三角形纸片ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB、AC于点E、F，连接DE、DF．求证：四边形AEDF是菱形．
如图，在四边形ABCD中，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB=4，AD=6，求AC的长．
