题目内容
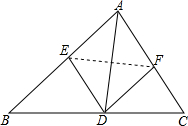 如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.
如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.考点:菱形的判定,翻折变换(折叠问题)
专题:证明题
分析:由∠BAD=∠CAD,AO=AO,∠AOE=∠AOF=90°证△AEO≌△AFO,推出EO=FO,得出平行四边形AEDF,根据EF⊥AD得出菱形AEDF.
解答: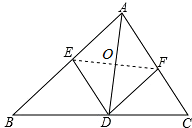 证明:∵AD平分∠BAC
证明:∵AD平分∠BAC
∴∠BAD=∠CAD
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
∵在△AEO和△AFO中
,
∴△AEO≌△AFO(ASA),
∴EO=FO
又∵A点与D点重合,
∴AO=DO,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形
∵点A与点D关于直线EF对称,
∵EF⊥AD,
∴平行四边形AEDF为菱形.
 证明:∵AD平分∠BAC
证明:∵AD平分∠BAC∴∠BAD=∠CAD
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
∵在△AEO和△AFO中
|
∴△AEO≌△AFO(ASA),
∴EO=FO
又∵A点与D点重合,
∴AO=DO,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形
∵点A与点D关于直线EF对称,
∵EF⊥AD,
∴平行四边形AEDF为菱形.
点评:本题考查了平行四边形的判定,菱形的判定,线段垂直平分线,全等三角形的性质和判定等知识点,注意:对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点A在数轴上,一只蚂蚁从A点出发沿数轴爬了6个单位长度到了原点,则点A表示的数是( )
| A、-6 | B、6 | C、12 | D、6或-6 |

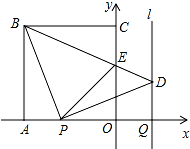 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
 已知:如图,在△ABC中,F是AB上一点,E是CD上一点,BE⊥DF于G,∠1=∠C,∠2+∠D=90°,试说明AB∥CD.
已知:如图,在△ABC中,F是AB上一点,E是CD上一点,BE⊥DF于G,∠1=∠C,∠2+∠D=90°,试说明AB∥CD.