题目内容
阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
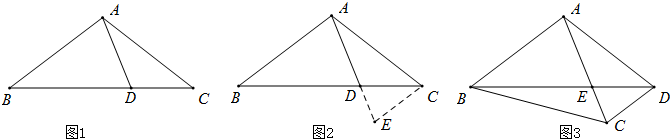
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.

考点:相似三角形的判定与性质,勾股定理,解直角三角形
专题:阅读型
分析:根据相似的三角形的判定与性质,可得
=
=
=2,根据等腰三角形的判定,可得AE=AC,根据正切函数,可得DF的长,根据直角三角形的性质,可得AB与DF的关系,根据勾股定理,可得答案.
| AB |
| DF |
| AE |
| EF |
| BE |
| DE |
解答: 解:∠ACE=75°,AC的长为3.
解:∠ACE=75°,AC的长为3.
过点D作DF⊥AC于点F.
∵∠BAC=90°=∠DFA,
∴AB∥DF,
∴△ABE∽△FDE,
∴
=
=
=2,
∴EF=1,AB=2DF.
在△ACD中,∠CAD=30°,∠ADC=75°,
∴∠ACD=75°,AC=AD.
∵DF⊥AC,
∴∠AFD=90°,
在△AFD中,AF=2+1=3,∠FAD=30°,
∴DF=AFtan30°=
,AD=2DF=2
.
∴AC=AD=2
,AB=2DF=2
.
∴BC=
=2
.
 解:∠ACE=75°,AC的长为3.
解:∠ACE=75°,AC的长为3.过点D作DF⊥AC于点F.
∵∠BAC=90°=∠DFA,
∴AB∥DF,
∴△ABE∽△FDE,
∴
| AB |
| DF |
| AE |
| EF |
| BE |
| DE |
∴EF=1,AB=2DF.
在△ACD中,∠CAD=30°,∠ADC=75°,
∴∠ACD=75°,AC=AD.
∵DF⊥AC,
∴∠AFD=90°,
在△AFD中,AF=2+1=3,∠FAD=30°,
∴DF=AFtan30°=
| 3 |
| 3 |
∴AC=AD=2
| 3 |
| 3 |
∴BC=
| AB2+AC2 |
| 6 |
点评:本题考查了相似三角形的判定与性质,利用了相似三角形的判定与性质,直角三角形的性质,勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 已知:如图,在△ABC中,F是AB上一点,E是CD上一点,BE⊥DF于G,∠1=∠C,∠2+∠D=90°,试说明AB∥CD.
已知:如图,在△ABC中,F是AB上一点,E是CD上一点,BE⊥DF于G,∠1=∠C,∠2+∠D=90°,试说明AB∥CD. 某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.
某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示. 我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b. 如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l. 如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为
如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为