题目内容
3.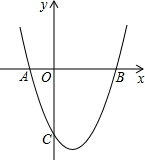 如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C′(0,c),且满足x12+x22+x1x2=7.
如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C′(0,c),且满足x12+x22+x1x2=7.(1)求m的取值范围;
(2)求抛物线的解析式.
分析 (1)利用判别式的意义得到△=m2-4(m-1)>0,解得m≠2,再利用函数图象得到抛物线与x轴的交点在x轴下方,则m-1<0,解得m<1,然后写出两个不等式的公共部分即可得到m的取值范围;
(2)根据根与系数的关系得到x1+x2=-m,x1x2=m-1,再变形x12+x22+x1x2=7得到(x1+x2)2-x1x2=7,则m2-(m-1)=7,解得m1=3,m2=-2,然后利用(1)m的范围即可确定满足条件的m的值,从而得到二次函数解析式.
解答 解:(1)根据题意得△=m2-4(m-1)>0,即(m-2)2>0,
∴m≠2,
∵抛物线与x轴的交点在x轴下方,
∴m-1<0,解得m<1,
∴m的取值范围为m<1且m≠2;
(2)根据题意得x1+x2=-m,x1x2=m-1,
∵x12+x22+x1x2=7,
∴(x1+x2)2-x1x2=7,
∴m2-(m-1)=7,
即m2-m-6=0,解得m1=3,m2=-2,
∵m<1且m≠2,
∴m=-2,
∴抛物线解析式为y=x2-2m-3.
点评 本题考查了抛物线与x轴的交点问题:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象与x轴的交点个数由△=b2-4ac决定;利用二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了根与系数的关系.

练习册系列答案
相关题目
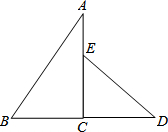 如图,是一副三角板组成的图形.
如图,是一副三角板组成的图形.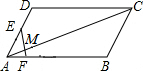 已知:如图,?ABCD中E为AD的中点,AF:AB=1:6,EF与AC交于M.求:AM:AC.
已知:如图,?ABCD中E为AD的中点,AF:AB=1:6,EF与AC交于M.求:AM:AC.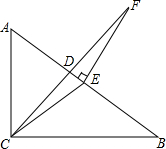 如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.
如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.