题目内容
8.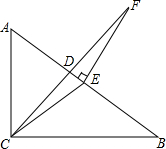 如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.
如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.
分析 由三角形内角和定理和已知条件得出∠A=∠ACE,得出∠DCE=∠A-45°,再由三角形的外角性质得出∠F=∠A-45°,即可得出结论.
解答 证明:∵CD是角平分线,
∴∠ACD=$\frac{1}{2}$∠ACB=45°,
∵∠ACB=90°,
∴∠A+∠B=90°,∠ACE+∠ECB=90°,
∵∠ECB=∠B,
∴∠A=∠ACE,
∴∠DCE=∠ACE-∠ACD=∠A-45°,
∵EF⊥AB,
∴∠DEF=90°,
∵∠CDE=∠A+45°=∠F+90°,
∴∠F=∠A-45°,
∴∠F=∠DCE.
点评 本题考查了三角形内角和定理、三角形的外角性质;熟练掌握三角形内角和定理和三角形的外角性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
17.已知2是关于x的方程:x2-x+a=0的一个解,则2a-1的值是( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
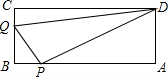 如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?
如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?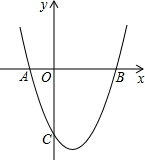 如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C′(0,c),且满足x12+x22+x1x2=7.
如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C′(0,c),且满足x12+x22+x1x2=7.
 已知,A(4,-1),B(2,-4),在x轴上找一点C,y轴上找一点D,使|AC+CD+BD|最小,求这个最小值.
已知,A(4,-1),B(2,-4),在x轴上找一点C,y轴上找一点D,使|AC+CD+BD|最小,求这个最小值.