题目内容
18.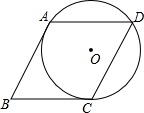 如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.
如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.
分析 连接OA、OC、OB.由切线的性质可知∠OAB=90°,然后证明△AOB≌△COB,从而得到∠OCB=∠OAB=90°,于是得到∠ABC+∠AOC=180°然后根据圆周角定理和菱形的性质可知∠AOC=2∠ABC,从而可求得∠AOC=60°.
解答 解:如图所示:连接OA、OC、OB.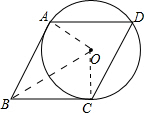
∵BA是圆O的切线,
∴OA⊥AB.
∴∠BAO=90°.
∵四边形ABCD是菱形,
∴AB=BC,∠ABC=∠ADC.
在△AOB和△COB中,
$\left\{\begin{array}{l}{AB=CB}\\{OA=OC}\\{OB=OB}\end{array}\right.$,
∴△AOB≌△COB.
∴∠OCB=∠OAB=90°.
∴∠ABC+∠AOC=180°.
又∵∠ADC=$\frac{1}{2}$∠AOC,
∴∠AOC=2∠ABC.
∴3∠AOC=180°.
∴∠AOC=60°.
点评 本题主要考查的是切线的性质、菱形的性质、全等三角形的性质和判定,证得∠AOC=2∠ABC、∠ABC+∠AOC=180°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.小丽连续两次掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则两次向上的一面的点数之和大于3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{31}{36}$ | D. | $\frac{2}{3}$ |
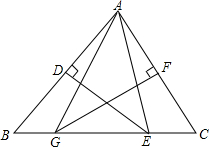 如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长?
如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长? 如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.
如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.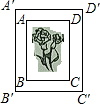 如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?
如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么? 已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?
已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$? 如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.
如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.