题目内容
7.当x取何值时,下列分式值为零?(1)$\frac{|x|-2}{{x}^{2}-4x+4}$;(2)$\frac{(x+3)(x-6)}{2|x|-6}$.
分析 分式值为零的条件是分式的分子为零,分母不为0.
解答 解:(1)∵分式的值为0,
∴|x|-2=0,且x2-4x+4≠0.
解得:x=-2.
∴当x=-2时,分式$\frac{|x|-2}{{x}^{2}-4x+4}$的值为零.
(2))∵分式的值为0,
∴(x+3)(x-6)=0,且2|x|-6≠0.
解得:x=6.
∴当x=6时,分式$\frac{(x+3)(x-6)}{2|x|-6}$的值为零.
点评 本题主要考查的是分式值为零的条件,掌握分式值为零的条件是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O的半径为1,弦AB=$\sqrt{2}$,则圆周角∠ACB=135°.
如图,⊙O的半径为1,弦AB=$\sqrt{2}$,则圆周角∠ACB=135°.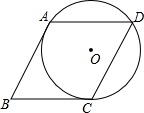 如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.
如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.