题目内容
16.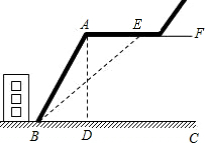 某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)
某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)
分析 连接BE,过E作EN⊥BC于N,则四边形AEND是矩形,有NE=AD,AE=DN,在Rt△ADB和Rt△BEN中都已知一边和一个锐角,满足解直角三角形的条件,可求出AD和BD、AE的长.
解答 解: 在Rt△ADB中,AB=30米∠ABC=60°
在Rt△ADB中,AB=30米∠ABC=60°
AD=AB•sin∠ABC=30×sin66°=30×0.91=27.3(米),
DB=AB•cos∠ABC=30×cos66°=30×0.41=12.3(米).
连接BE,过E作EN⊥BC于N,如图所示:
∵AE∥BC,
∴四边形AEND是矩形NE=AD≈27.3米,
在Rt△ENB中,∠EBN=45°时,BN=EN=AD=27.3米,
∴AE=DN=BN-BD=27.3-12.3=15米
答:AE是15米.
点评 本题考查了解直角三角形的应用;通过构造直角三角形和矩形是解决问题的关键.

练习册系列答案
相关题目
7.如果5x=m,5y=n,那么5x-y等于( )
| A. | m+n | B. | m-n | C. | mn | D. | $\frac{m}{n}$ |
11.计算2-2(1-a)的结果是( )
| A. | a | B. | -a | C. | 2a | D. | -2a |
8.在△ABC中,∠B=∠C=30°,BC=6,则△ABC的内切圆半径与△ABC的外接圆的直径的和为( )
| A. | 6-$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6-3$\sqrt{3}$ | D. | 6+$\sqrt{3}$ |
5.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | 3a2b2÷a2b2=3ab | C. | (-a2)2=a4 | D. | (-m3)2=m9 |
6.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则$\widehat{BC}$的度数是( )


| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
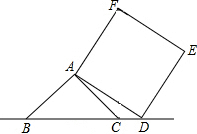 如图,已知等腰Rt△ABC中,∠BAC=90°,D为BC延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF
如图,已知等腰Rt△ABC中,∠BAC=90°,D为BC延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF 如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.