题目内容
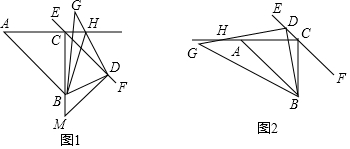
4.已知在△ABC中,AC=BC,AC⊥BC于点C,过点C作直线EF∥AB,点D在直线EF上,连接BD,过点D作GD⊥BD,交直线AC于点H,连接BG.(1)如图1所示,当点D在射线CF上,点H在射线AC上时,连接BH,过点D作MD⊥CD,交CB的延长线于点M.求证:∠GBH+∠G=∠M;
(2)如图2所示,当点D在射线CE上,点H在射线CA上时,试判断并证明DH与BD之间的数量关系.
分析 (1)如图1中,作DN⊥EM于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB,推出DH=BD,推出△BDH是等腰直角三角形,由此即可解决问题;
(2)如图2中,作DN⊥BC于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB即可;
解答 (1)证明:如图1中,作DN⊥EM于N,DP⊥AC于P.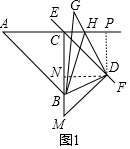
∵CA=CB,∠ACB=90°,
∴∠A=∠ABC=45°,
∵EF∥AB,
∴∠DCP=∠A=∠DCB=45°,
∵DN⊥EM于N,DP⊥AC于P,
∴DP=DN
∵∠PCN=∠DNC=∠DPC=90°,
∴四边形PCND是矩形,
∴∠PDN=∠BDH=90°,
∴∠PDH=∠BDN,
∴△DPH≌△DNB,
∴DH=BD,
∴△BDH是等腰直角三角形,
∴∠BHD=45°,
∵∠BHD=∠GBH+∠G,
∴∠GBH+∠G=45°,
∵DM⊥DC,
∴∠M=∠DCM=45°,
∴∠GBH+∠G=∠M.
(2)如图2中,作DN⊥BC于N,DP⊥AC于P.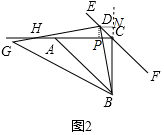
∵CA=CB,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵EF∥AB,
∴∠DCP=∠BAC=∠DCN=45°,
∵DN⊥EM于N,DP⊥AC于P,
∴DP=DN
∵∠PCN=∠DNC=∠DPC=90°,
∴四边形PCND是矩形,
∴∠PDN=∠BDH=90°,
∴∠PDH=∠BDN,
∴△DPH≌△DNB,
∴DH=BD,
点评 本题考查等腰直角三角形的性质、平行线的性质、全等三角形的判定和性质、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考考常考题型.

练习册系列答案
相关题目
15.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列说法中,正确的是( )
| A. | 任何数都有两个平方根 | B. | 9的平方根只有3 | ||
| C. | (-2)3的立方根为2 | D. | 0.04的算术平方根为0.2 |
9. 如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
 如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )| A. | 25° | B. | 40° | C. | 50° | D. | 80° |
13. 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
14.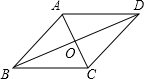 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
 已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由.
已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由. 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图: