题目内容
14．
已知，在四边形ABCD中，AB=AD，∠B=∠D，请说明CB=CD的理由．
分析 作辅助线BD，构建等腰△ABD．在△ABD中，根据等腰三角形的性质知两个底角∠ADB=∠ABD，再根据已知条件∠B=∠D，从而求得∠CBD=∠CDB，易证明CB=CD（等角对等边）．
解答 
解：连接BD．
∵AB=AD，
∴∠ADB=∠ABD（等边对等角）；
又∵∠B=∠D，
∴∠B-∠ABD=∠D-∠ADB，
即∠CBD=∠CDB，
∴CB=CD（等角对等边）．
点评 本题考查了全等三角形的判定与性质．借助于辅助线BD将隐含在题中的条件“△ABD是等腰三角形”给挖掘了出来，给证明∠CBD=∠CDB提供了有力的依据．
练习册系列答案
阅读快车系列答案
相关题目
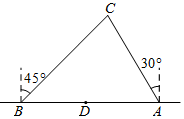如图，两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍船只停在C处海域，AB=60（$\sqrt{3}$+1）海里，在B处测得C在北偏东45°反向上，A处测得C在北偏西30°方向上，在海岸线AB上有一灯塔D，测得AD=100海里．
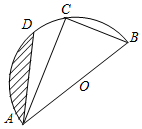已知：如图，AB为半圆O的直径，C、D是半圆O上的两点，若直径AB的长为4，且BC=2，∠DAC=15°．