题目内容
20.图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画一符合要求的图形.要求:所画图形各顶点必须与方格纸中的小正方形顶点重合.
(1)画一个周长为4$\sqrt{2}$+4的直角三角形;
(2)画一个周长为15+3$\sqrt{5}$,面积15的三角形.

分析 (1)根据勾股定理,作出2$\sqrt{2}$的线段作为直角边,然后作出等腰直角三角形即可;
(2)根据网格结构以及勾股定理作出以3和6为直角边的直角三角形的斜边作为新三角形的一边,从而得到边3$\sqrt{5}$,再根据勾股定理作出以3、4为直角边的斜边作为另一边,然后在网格边上找出长为10的边,连接即可.
解答  解:(1)如图所示,△ABC的周长为4$\sqrt{2}$+4的直角三角形;
解:(1)如图所示,△ABC的周长为4$\sqrt{2}$+4的直角三角形;
(2)如图,DE=$\sqrt{{3}^{2}+{4}^{2}}$=5,DF=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
EF=10,
△DEF的周长=5+3$\sqrt{5}$+10=15+3$\sqrt{5}$,
面积=$\frac{1}{2}$×10×3=15,
所以△DEF即为所求三角形.
点评 本题考查了勾股定理,复杂作图,熟练掌握网格结构以及勾股定理作出相关长度的线段是解题的关键,难点在于(2)根据3、4、5是勾股作出不在网格边上的长为5的线段.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | ±$\sqrt{9}$=3 | C. | $\sqrt{(-3)^2}$=±3 | D. | ±$\sqrt{16}$=±4 |
12.下列说法中,不正确的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 在同一平面内,垂直于同一条直线的两条直线互相平行 | |
| C. | 如果∠1与∠2是同位角,那么∠1=∠2 | |
| D. | 平移不改变图形的形状和大小 |
9.若(9+x2)(x+3)( )=81-x4,则括号内应填入的代数式为( )
| A. | x-3 | B. | 3-x | C. | 3+x | D. | x-9 |
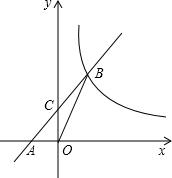 如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.
如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值. 如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.
如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.