题目内容
11. 如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.
如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.
分析 每个小正方形的边长均为1,利用勾股定理得出AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,据此画出△ABC,△ABC的面积=正方形的面积-3个小直角三角形的面积,即可得出结果.
解答 解: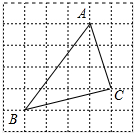 由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
∴画△ABC如图所示:
△ABC的面积=4×4-$\frac{1}{2}$×4×3-$\frac{1}{2}$×4×1-$\frac{1}{2}$×3×1=6.5.
点评 本题考查了勾股定理、直角三角形的面积.在解答(2)题时,利用了“分割法”来求△ABC的面积.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | (6a9)÷(3a3)=2a3 | B. | (-4x3y)÷(2x2y)=-2x | C. | (x-y)3÷(y-x)=(y一x)2 | D. | am÷an÷ap=am-n+p |
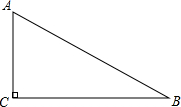 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.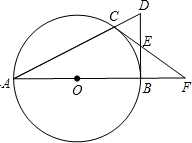 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F. (1)画∠ACE,使得∠ACE=∠BAC且∠ACE的边CE交AB于点E;
(1)画∠ACE,使得∠ACE=∠BAC且∠ACE的边CE交AB于点E;
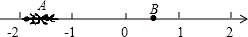 如图所示,一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示$-\sqrt{2}$,设点B所表示的数为m,则|m-1|的值是1-m.
如图所示,一只蚂蚁从点A沿数轴向右爬2个单位到达点B,点A表示$-\sqrt{2}$,设点B所表示的数为m,则|m-1|的值是1-m.