题目内容
1.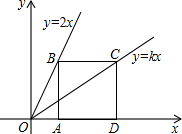 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 设正方形的边长为a,根据正方形的性质分别表示出B,C两点的坐标,再将C的坐标代入函数中从而可求得k的值.
解答 解:设正方形的边长为a,则B的纵坐标是a,
把点B代入直线y=2x的解析式,设点B的坐标为($\frac{a}{2}$,a),则点C的坐标为($\frac{a}{2}$+a,a),
把点C的坐标代入y=kx中得,a=k($\frac{a}{2}$+a),
解得k=$\frac{2}{3}$,
故选:B.
点评 本题考查的是一次函数图象上点的坐标特征、正方形的性质,掌握一次函数图象上点的坐标特征是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
18. 如图,表示点C到直线AB的距离的是线段( )的长度.
如图,表示点C到直线AB的距离的是线段( )的长度.
 如图,表示点C到直线AB的距离的是线段( )的长度.
如图,表示点C到直线AB的距离的是线段( )的长度.| A. | CD | B. | CB | C. | CA | D. | DA |
9.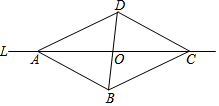 如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )
如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )
 如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )
如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )| A. | AB=CD,AO=OC | B. | AB=BD,∠BAD=∠DCB | C. | AB∥BC,BC=BD | D. | OD=OB,∠CDB=∠BCD |
16.某城市用电收费实行阶梯电价,收费标准如下表所示,用户5月份交电费45元,则所用电量为20度.
| 月用电量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准(元/度) | 2.00 | 2.50 | 3.00 |
6. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )| A. | (1,1) | B. | (1,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
13.已知实数x、y、z满足:(x+z)2-4(x-y)(y+z)=0,下列式子一定成立的是( )
| A. | x+y-z=0 | B. | x+y+2z=0 | C. | y-z-2x=0 | D. | -z+x-2y=0 |
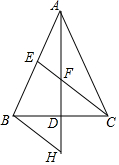 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,CE是边AB的中线,交AD于点F,点H在AD延长线上,且FH=AF,连接BH.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,CE是边AB的中线,交AD于点F,点H在AD延长线上,且FH=AF,连接BH.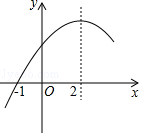 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③a+b+c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③a+b+c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )