题目内容
6. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )| A. | (1,1) | B. | (1,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
分析 连接CB,根据位似变换的性质得到A为OC的中点,根据平行线的性质得到OB=OD,根据等腰直角三角形的性质计算即可.
解答 解:连接CB,
∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,
∴A为OC的中点,
∵∠OCD=90°,
∴∠OAB=90°,
∴AB∥CD,
∴OB=OD,
∵∠OCD=90°,CO=CD,
∴CB⊥OD,OB=BC=1,
∴点C的坐标为(1,1),
故选:A.
点评 本题考查的是位似变换的性质、等腰直角三角形的性质,两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.

练习册系列答案
相关题目
17.计算(x+y)(y-x)=( )
| A. | x2-y2 | B. | x2+y2 | C. | y2-x2 | D. | (x-y)2 |
14.如表为某市居民每月用水收费标准,(单位:元/m3).
(1)某用户1月用水10立方米,共交水费23元,则a=2.3元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
| 用水量 | 单价 |
| 0<x≤22 | a |
| 剩余部分 | a+1.1 |
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
1.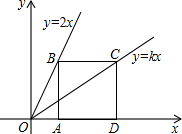 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
11.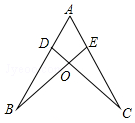 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,有下列条件:①AB=AC;②DC=BE;③∠B=∠C,从中选择两个条件判定△ABE≌△ACD,是真命题的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.下列计算结果正确的是( )
| A. | 2+$\sqrt{5}$=2$\sqrt{5}$ | B. | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C. | (-2a2)3=-6a6 | D. | (x+1)2=x2+1 |
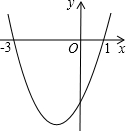 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )