题目内容
9.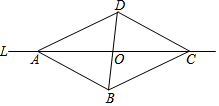 如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )
如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( )| A. | AB=CD,AO=OC | B. | AB=BD,∠BAD=∠DCB | C. | AB∥BC,BC=BD | D. | OD=OB,∠CDB=∠BCD |
分析 由翻折的性质可知;AD=AB,DC=BC,∠DAC=∠BAC,由平行线的性质可知∠DCA=∠BAC,从而得到∠DAC=∠DCA,故AD=CD,从而可知四边形ABCD为菱形,最后依据菱形的性质判断即可.
解答 解:由翻折的性质可知:AD=AB,DC=BC,∠DAC=∠BAC.
∵AB∥CD,
∴∠DCA=∠BAC,
∴∠DAC=∠DCA,
∴AD=CD,
∴AB=BC=CD=AD,
∴四边形ABCD为菱形,
∴AB=CD,AC⊥BD,AO=CO.
故选:A.
点评 本题主要考查的是翻折的性质、菱形的性质和判定、等腰三角形的判定、平行线的性质,证得四边形ABCD为菱形是解题的关键.

练习册系列答案
相关题目
6.如图是一个运算程序的示意图,若开始入x的值为81,则第2015次输出的结果为( )


| A. | 3 | B. | 27 | C. | 9 | D. | 1 |
7.二元一次方程2x-y=-1与x+2y=12所对应直线的交点坐标是( )
| A. | (-1,-1) | B. | (2,5) | C. | (1,6) | D. | (-2,5) |
17.计算(x+y)(y-x)=( )
| A. | x2-y2 | B. | x2+y2 | C. | y2-x2 | D. | (x-y)2 |
4. 如图所示的几何体,从正面看到所得的图形是( )
如图所示的几何体,从正面看到所得的图形是( )
 如图所示的几何体,从正面看到所得的图形是( )
如图所示的几何体,从正面看到所得的图形是( )| A. |  | B. |  | C. |  | D. |  |
14.如表为某市居民每月用水收费标准,(单位:元/m3).
(1)某用户1月用水10立方米,共交水费23元,则a=2.3元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
| 用水量 | 单价 |
| 0<x≤22 | a |
| 剩余部分 | a+1.1 |
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费60.8元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费71元.请问该用户实际用水多少立方米?
1.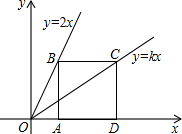 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
19.下列分式的变形正确的是( )
| A. | $\frac{a}{a-1}-\frac{1}{a-1}=1$ | B. | $\frac{m}{{{m^2}+1}}=\frac{1}{m+1}$ | C. | $\frac{{{x^2}-1}}{x-1}=x-1$ | D. | $\frac{-a-1}{a+1}=-\frac{a-1}{a+1}$ |