题目内容
 如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=
如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=考点:角平分线的定义
专题:
分析:先根据∠AOB=α,∠COD=β可知∠AOD=∠COD+∠AOC=β+∠AOC,∠BOC=∠AOB+∠AOC=α+∠AOC,∠BOD=∠AOD+∠BOC-∠AOC=α+β+∠AOC,再根据OM为∠AOD的平分线,ON为∠BOC的平分线,得出∠BON=
∠BOC,∠DOM=
∠AOD,由∠MON=∠BOD-∠BON-∠DOM即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠AOB=α,∠COD=β,
∴∠AOD=∠COD+∠AOC=β+∠AOC,∠BOC=∠AOB+∠AOC=α+∠AOC,
∴∠BOD=∠AOD+∠BOC-∠AOC=α+β+∠AOC.
∵OM为∠AOD的平分线,ON为∠BOC的平分线,
∴∠BON=
∠BOC,∠DOM=
∠AOD,
∴∠MON=∠BOD-∠BON-∠DOM
=α+β+∠AOC-
∠BOC-
∠AOD
=α+β+∠AOC-
(∠BOC+∠AOD)
=α+β+∠AOC-
(α+β+2∠AOC)
=α+β+∠AOC-
α-
β-∠AOC
=
(α+β).
故答案为:
(α+β).
∴∠AOD=∠COD+∠AOC=β+∠AOC,∠BOC=∠AOB+∠AOC=α+∠AOC,
∴∠BOD=∠AOD+∠BOC-∠AOC=α+β+∠AOC.
∵OM为∠AOD的平分线,ON为∠BOC的平分线,
∴∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠BOD-∠BON-∠DOM
=α+β+∠AOC-
| 1 |
| 2 |
| 1 |
| 2 |
=α+β+∠AOC-
| 1 |
| 2 |
=α+β+∠AOC-
| 1 |
| 2 |
=α+β+∠AOC-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
相关题目
下列实数中,是无理数的是( )
A、
| |||
| B、-0.3 | |||
C、
| |||
D、
|
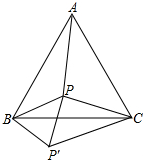 已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.
已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置. 如图,在平行四边形ABCD中对角线AC、BD相交于O,EF⊥AC点D,垂足EF分别交AB、CD于E、F,且BE=OE=
如图,在平行四边形ABCD中对角线AC、BD相交于O,EF⊥AC点D,垂足EF分别交AB、CD于E、F,且BE=OE= 如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论.
如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论. 如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.
如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.