题目内容
 如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论.
如图,在矩形ABCD中,∠ABC的角平分线交对角线AC于点M,ME⊥AB,MF⊥BC,垂足分别是E,F.判定四边形EBFM的形状,并证明你的结论.考点:正方形的判定
专题:
分析:首先证得四边形EBFM为矩形,再进一步利用角平分线的性质得出ME=MF,证得结论成立即可.
解答:四边形EBFM是正方形.
证明:∵矩形ABCD,
∴∠ABC=90°,
∵MF⊥BC,ME⊥AB,
∴∠BFM=∠MEB=90°,
∵∠ABC=∠BFM=∠MEB=90°,
∴四边形EBFM为矩形,
∵BM平分∠ABC,
∴ME=MF,
∴四边形EBFM为正方形.
证明:∵矩形ABCD,
∴∠ABC=90°,
∵MF⊥BC,ME⊥AB,
∴∠BFM=∠MEB=90°,
∵∠ABC=∠BFM=∠MEB=90°,
∴四边形EBFM为矩形,
∵BM平分∠ABC,
∴ME=MF,
∴四边形EBFM为正方形.
点评:此题考查正方形的判定,矩形的性质以及角平分线的性质,结合图形,利用已知条件灵活解决问题.

练习册系列答案
相关题目
下列运算中正确的是( )
| A、2x+3y=5xy |
| B、x8÷x2=x4 |
| C、(x2y)3=x6y3 |
| D、2x3•x2=2x6 |
 如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=
如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=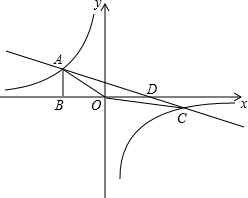 如图,反比例函数
如图,反比例函数 小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?
小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?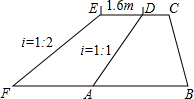 某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据
某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据