题目内容
下表中有两种移动电话计费方式.
设一个月内用移动电话主叫为t min(t是正整数),你能从中发现如何根据主叫时间选择省钱的计费方式吗?当t满足 时,选择方式一,当t满足 时,选择方式二.
| 月使用费/元 | 主叫限定时间/min | 主叫超时费/(元/min) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
考点:一元一次方程的应用
专题:应用题
分析:根据计费方式表示出两种方式的收费,分类讨论得到结果即可.
解答:解:由题意,得①当150<t<350时,方式一收费:58+0.25(t-150)=(0.25t+20.5)元;
②当t>350时,方式一收费:58+0.25(t-150)=(0.25t+20.5)元;
③方式二当t>350时收费:88+0.19(t-350)=(0.19t+21.5)元,
当t≤150时,方式一的付费为58元,方式二的付费为88元,
∵58<88,∴方式一计费省;
当150<t<350时,方式一的计费由58元增加到108元,方式二是88元,
当58+0.25(t-150)=88时,
解得:t=270,
∴t<270时,方式一省钱,t=270时,两种方式一样省钱,270<t<350时,方式二省钱;
当t≥350时,0.25t+20.5-(0.19t+21.5)=0.06t-1>0,
∴方式二省钱,
则综上所述,t<270时,方式一省钱,t=270时,两种方式一样省钱,t>270时方式二省钱.
故答案为:t<270;t>270
②当t>350时,方式一收费:58+0.25(t-150)=(0.25t+20.5)元;
③方式二当t>350时收费:88+0.19(t-350)=(0.19t+21.5)元,
当t≤150时,方式一的付费为58元,方式二的付费为88元,
∵58<88,∴方式一计费省;
当150<t<350时,方式一的计费由58元增加到108元,方式二是88元,
当58+0.25(t-150)=88时,
解得:t=270,
∴t<270时,方式一省钱,t=270时,两种方式一样省钱,270<t<350时,方式二省钱;
当t≥350时,0.25t+20.5-(0.19t+21.5)=0.06t-1>0,
∴方式二省钱,
则综上所述,t<270时,方式一省钱,t=270时,两种方式一样省钱,t>270时方式二省钱.
故答案为:t<270;t>270
点评:此题考查了一元一次方程的应用,弄清两种方式的计费方式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法错误的是( )
| A、等腰三角形底边上的高所在的直线是对称轴 |
| B、等腰三角形底边上的中线所在的直线是对称轴 |
| C、等腰三角形顶角的平分线所在的直线是对称轴 |
| D、等腰三角形一内角平分线所在的直线是对称轴 |
某种长途电话的收费方式如下,按通电话的第一分钟收费m元,之后的每一分钟收费n元,如果某人打长途电话按收费10元钱,则此人打长途电话的时间为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在同一坐标系中,函数y=kx与y=
x-k的图象大致是( )
| 4 |
| 5 |
A、 |
B、 |
C、 |
D、 |
 如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=
如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=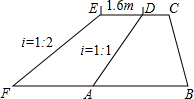 某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据
某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据