题目内容
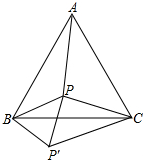 已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.
已知,P为等边三角形内一点,且BP=3,PC=4,将BP绕点B顺时针旋转60°至BP′的位置.(1)试判断△BPP′的形状,并说明理由;
(2)若P′C=5,求PA.
考点:全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质
专题:
分析:(1)直接运用判定定理即可解决问题.
(2)证明△ABP≌△CBP′,即可解决问题.
(2)证明△ABP≌△CBP′,即可解决问题.
解答: 证明:(1)∵BP=BP′,∠PBP′=60°,
证明:(1)∵BP=BP′,∠PBP′=60°,
∴△BPP′为等边三角形.
(2)∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC;
∵∠PBP′=60°,
∴∠ABP=∠CBP′;
在△ABP与△CBP′中,
,
∴△ABP≌△CBP′(SAS),
∴PA=P′C=5.
 证明:(1)∵BP=BP′,∠PBP′=60°,
证明:(1)∵BP=BP′,∠PBP′=60°,∴△BPP′为等边三角形.
(2)∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC;
∵∠PBP′=60°,
∴∠ABP=∠CBP′;
在△ABP与△CBP′中,
|
∴△ABP≌△CBP′(SAS),
∴PA=P′C=5.
点评:该题主要考查了等边三角形的性质、全等三角形的判定及其性质等几何知识点的应用问题;牢固掌握定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法错误的是( )
| A、等腰三角形底边上的高所在的直线是对称轴 |
| B、等腰三角形底边上的中线所在的直线是对称轴 |
| C、等腰三角形顶角的平分线所在的直线是对称轴 |
| D、等腰三角形一内角平分线所在的直线是对称轴 |
 如图,将面积为a2的小正方形和面积为b2的大正方形放在一起(b>a>0),用a,b表示△ABC的面积为
如图,将面积为a2的小正方形和面积为b2的大正方形放在一起(b>a>0),用a,b表示△ABC的面积为 如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=
如图,已知∠AOB=α,∠COD=β,OM为∠AOD的平分线,ON为∠BOC的平分线,则∠MON=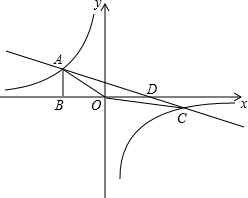 如图,反比例函数
如图,反比例函数 小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?
小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?