题目内容
10. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和.
分析 如图所示,由三角形外角的性质可知:∠A+∠B+∠C=∠IKD,∠E+∠F+∠G=∠HND,然后由多边形的内角和公式可求得答案.
解答 解:如图所示:
由三角形的外角的性质可知:∠A+∠B=∠AJC,∠AJC+∠C=∠IKD,
∴∠A+∠B+∠C=∠IKD.
同理:∠E+∠F+∠G=∠HND.
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠I+∠H=∠IKD+∠D+∠HND+∠I+∠H=(5-2)×180°=3×180°=540°.
点评 本题主要考查的是三角形外角的性质和多边形的内角和公式的应用,利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
18.下列说法中正确的是( )
| A. | 一个数的绝对值等于它本身,则这个数是正数 | |
| B. | 一个数的绝对值等于它的相反数,则这个数是负数 | |
| C. | 一个数的绝对值不可能等于零 | |
| D. | 一个数的绝对值不可能为负数 |
20.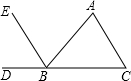 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )
 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )| A. | ∠C=∠ABE | B. | ∠A=∠ABE | C. | ∠C=∠ABC | D. | ∠A=∠EBD |
 如图,由边长为1个单位长度的小正方形组成的8×8网格和△ABC在平面直角坐标系中.
如图,由边长为1个单位长度的小正方形组成的8×8网格和△ABC在平面直角坐标系中.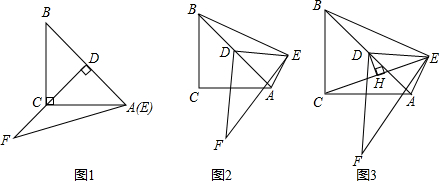
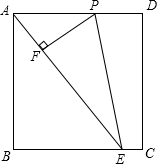 如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.
如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.