题目内容
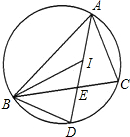 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.考点:三角形的内切圆与内心
专题:
分析:要证明ID=BD,只要求得∠BID=∠IBD即可.
解答:证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
点评:本题考查了三角形的内切圆和内心的,以及等腰三角形的判定与性质,同弧所对的圆周角相等.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
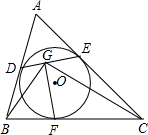 已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF.
已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF. 如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;
如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证; 如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6
如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6