题目内容
半径为4的圆内接正三角形的边长为 ,面积为 .
考点:正多边形和圆
专题:
分析:欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长,再根据三角形的面积公式求出面积即可.
解答:解:如图所示:

∵半径为4的圆的内接正三角形,
∴在Rt△BOD中,OB=4,∠OBD=30°,
∴BD=cos30°×OB=
×4=2
,
∵BD=CD,
∴BC=2BD=4
,
故它的内接正三角形的边长为4
,
OD=
OB=2,
即AD=4+2=6,
所以△ABC的面积为
×4
×6=12
,
故答案为:4
,12
.

∵半径为4的圆的内接正三角形,
∴在Rt△BOD中,OB=4,∠OBD=30°,
∴BD=cos30°×OB=
| ||
| 2 |
| 3 |
∵BD=CD,
∴BC=2BD=4
| 3 |
故它的内接正三角形的边长为4
| 3 |
OD=
| 1 |
| 2 |
即AD=4+2=6,
所以△ABC的面积为
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:4
| 3 |
| 3 |
点评:本题主要考查了正多边形和圆,根据正三角形的性质得出∠OBD=30°是解题关键,此题难度一般,是一道比较不错的试题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
| A、65元 | B、80元 |
| C、100元 | D、104元 |
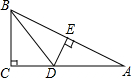 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
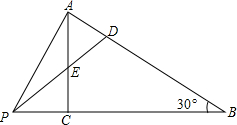 如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.
如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.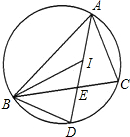 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.