题目内容
15.一组按规律排列的式子:a2,$\frac{{a}^{4}}{2}$,$\frac{{a}^{6}}{3}$,$\frac{{a}^{8}}{4}$,…,则第2016个式子是( )| A. | $\frac{{a}^{2016}}{2015}$ | B. | $\frac{{a}^{2016}}{2016}$ | C. | $\frac{{a}^{4030}}{2015}$ | D. | $\frac{{a}^{4032}}{2016}$ |
分析 分母的变化规律是1、2、3、4…,指数的变化规律四2、4、6、8…,根据此规律即可求出第2016个式子.
解答 解:由a2,$\frac{{a}^{4}}{2}$,$\frac{{a}^{6}}{3}$,$\frac{{a}^{8}}{4}$,…,可知
第n个式子为:$\frac{{a}^{2n}}{n}$
∴第2016个式子为$\frac{{a}^{4032}}{2016}$
故选(D)
点评 本题考查数字规律问题,解题的关键是根据题意找出规律,本题属于基础题型.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
10.若a+3=0,则a=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
4.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | $\root{3}{-8}$=-2 |
5.如果点(a,b)在直线y=-x+1上,二次函数y=ax2+bx的图象必经过( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
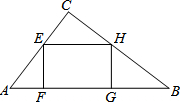 如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.
如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.