题目内容
20. 如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 过点A作AF⊥BC,垂足为点F,利用三角函数求得BF、AF、EC的长,从而求得下底BC的长,根据梯形的面积公式即可求得其面积.
解答 解:过点A作AF⊥BC,垂足为点F.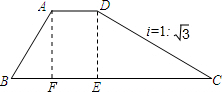
在Rt△ABF中,∠B=60°,AB=6,
∴AF=ABsin∠B
=6sin60°
=3$\sqrt{3}$.
BF=ABcos∠B
=6cos60°
=3.
∵AD∥BC,AF⊥BC,DE⊥BC,
∴四边形AFED是矩形,
∴DE=AF=3$\sqrt{3}$,FE=AD=4.
在Rt△CDE中,i=$\frac{ED}{EC}$,
∴EC=$\sqrt{3}$ED=$\sqrt{3}$×3$\sqrt{3}$=9,
∴BC=BF+FE+EC=3+5+9=17.
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)•DE
=$\frac{1}{2}$(5+17)×3$\sqrt{3}$
≈57.2.
答:拦水坝的横断面ABCD的面积约为57.2面积单位.
点评 本题考查了解直角三角形的应用--坡度坡角问题,熟悉三角函数和梯形面积公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.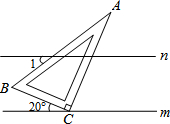 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
8.下列各式中,运算正确的是( )
| A. | a8÷a4=a2 | B. | (a4)3=a7 | C. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{6}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=2 |
 如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6.
如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6. 如图所示的电路中,开关k1、k2是否闭合是等可能的,则随机的闭合开关,两只灯泡能同时发光的概率是$\frac{1}{4}$.
如图所示的电路中,开关k1、k2是否闭合是等可能的,则随机的闭合开关,两只灯泡能同时发光的概率是$\frac{1}{4}$.