��Ŀ����
11����ƽ��ֱ������ϵ�У�ֱ��x=-$\sqrt{3}x$+4$\sqrt{3}$�ֱ�x�ᣬy���ڵ�A��B��CΪAB���е㣬����D��ԭ��O��������ÿ��1����λ���ٶ����յ�A�˶�������D��OA�Ĵ��ߣ��ֱ�ֱ��AB��OC�ڵ�P��Q����PQΪһ�����������������EPQ����ͼ��ʾ�����D���˶�ʱ��Ϊt���룩����EPQ�͡�OBC�ص����ֵ����ΪS��ƽ����λ������1�����C�����ꣻ
��2������Eǡ����y���ϣ���t��ֵ��
��3����0��t��2ʱ����S����t�ĺ�����ϵʽ������S�����ֵ��
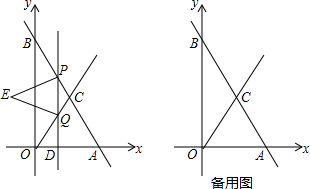
���� ��1�����ֱ��y=-$\sqrt{3}x$+4$\sqrt{3}$����������Ľ������꣬����CΪAB���е㣬�����C�����ꣻ
��2�����ݵȱ������α���ߵĹ�ϵ�г���ʽ�����t��
��3������S=��EPQ�����-��EFH���������t��ʾ��S��������ֵ���ɣ�
��� �⣺��1��ֱ��y=-$\sqrt{3}x$+4$\sqrt{3}$��
��y=0ʱ��x=4��A��4��0����
x=0ʱ��y=4$\sqrt{3}$��B��0��4$\sqrt{3}$����
��CΪAB���е㣬
���C����������2��2$\sqrt{3}$��
��2��t���P���������Ϊ-$\sqrt{3}$t+4$\sqrt{3}$��
ֱ��OC�Ľ���ʽΪy=$\sqrt{3}$x��
��t���Q���������Ϊ$\sqrt{3}$t��
PQ=-$\sqrt{3}$t+4$\sqrt{3}$-$\sqrt{3}$t=-2$\sqrt{3}$t+4$\sqrt{3}$��
��E��y����ʱ��-2$\sqrt{3}$t+4$\sqrt{3}$=$\frac{2}{3}\sqrt{3}$t��
t=$\frac{3}{2}$��
��3���ߡ�EPQ�ǵȱ������Σ�PQ=-2$\sqrt{3}$t+4$\sqrt{3}$��
S��EPQ=$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$��-2$\sqrt{3}$t+4$\sqrt{3}$��2=3$\sqrt{3}$t2-12$\sqrt{3}$t+12$\sqrt{3}$��
��EFH�ı�FH�ϵĸ�Ϊ$\frac{\sqrt{3}}{2}$��-2$\sqrt{3}$t+4$\sqrt{3}$��-t=-4t+6��
S��EFH=$\frac{1}{2}$��$\frac{2}{3}\sqrt{3}$��-4t+6��2=$\frac{16}{3}$$\sqrt{3}$t2-16$\sqrt{3}$t+12$\sqrt{3}$��
S=S��EPQ-S��EFH
=��3$\sqrt{3}$t2-12$\sqrt{3}$t+12$\sqrt{3}$��-��$\frac{16}{3}$$\sqrt{3}$t2-16$\sqrt{3}$t+12$\sqrt{3}$��
=-$\frac{7}{3}$$\sqrt{3}$t2+4$\sqrt{3}$t��0��t��2����
��-$\frac{7}{3}$$\sqrt{3}$��0�����������ֵΪ$\frac{12\sqrt{3}}{7}$��
���� ���⿼�����һ�κ������ۺ�Ӧ�ú͵ȱ������ε����ʣ����������ͼ���г�������ϵʽ�ǽ���Ĺؼ������ʱ��ע��ȱ������ε�����ı�ʾ������������ã�

 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�| A�� | ��2��-3�� | B�� | ��-2��-3�� | C�� | ��-2��3�� | D�� | ��2��3�� |
 ��ͼ�������ŶԱ�ƽ�е�ֽ�������⽻�������һ���غϵIJ��ֹ�����һ���ı���
��ͼ�������ŶԱ�ƽ�е�ֽ�������⽻�������һ���غϵIJ��ֹ�����һ���ı���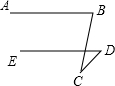 ��ͼ��ʾ��AB��DE�������C��AB��ED֮�⣬�����������䣬��ô��ABC����CDE���BCD֮�����������������ϵ����֤�����㻹�ܾͱ�������ʲô�µIJ��룿
��ͼ��ʾ��AB��DE�������C��AB��ED֮�⣬�����������䣬��ô��ABC����CDE���BCD֮�����������������ϵ����֤�����㻹�ܾͱ�������ʲô�µIJ��룿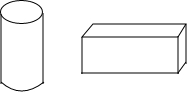 ��ͼ��ij������һ���ݻ�Ϊ100��L��Բ������ˮ�������ĸߵ��ڵ���ֱ��d��2������1L=1�������ף�������Ϊ�������һ�ֳ�����İ�װ�У����ݻ�Ϊ432L����Ϊ6���ף��ҳ�����֮��Ϊ2��1�������ְ�װ��������
��ͼ��ij������һ���ݻ�Ϊ100��L��Բ������ˮ�������ĸߵ��ڵ���ֱ��d��2������1L=1�������ף�������Ϊ�������һ�ֳ�����İ�װ�У����ݻ�Ϊ432L����Ϊ6���ף��ҳ�����֮��Ϊ2��1�������ְ�װ��������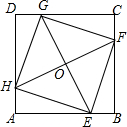 ��ͼ����������ABCD�У�E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA�ϵĵ㣬HA=EB=FC=GD������EG��FH������ΪO������EF��FG��GH��HE����֤���ı���EFGH�������Σ�
��ͼ����������ABCD�У�E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA�ϵĵ㣬HA=EB=FC=GD������EG��FH������ΪO������EF��FG��GH��HE����֤���ı���EFGH�������Σ�