题目内容
2. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形
如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形(1)求证:四边形ABCD为平行四边形;
(2)求证:AB=DC;
(3)若两张纸条宽分别为2cm和4cm,求$\frac{AB}{AD}$.
分析 (1)由AB∥CD,AD∥BC,得到四边形ABCD是平行四边形;
(2)由四边形ABCD是平行四边形得到AB=CD;
(3)由平行四边形的面积公式得到等积式,求得结果.
解答 (1)证明:由题意得:AB∥CD,AD∥BC,
∵两组对边分别平行,
∴四边形ABCD是平行四边形;
(2)由(1)证得四边形ABCD是平行四边形,
∵平行四边形的等边分别相等,
∴AB=CD;
(3)如图过点D作DE⊥AB于E,过点C作CF⊥AD于F,
∴?ABCD的面积=AB•DE=AD•CF,
∴$\frac{AB}{AD}$=$\frac{CF}{DE}$,
∵两张纸条宽分别为2cm和4cm,
∴CF=2,DE=4,
∴$\frac{AB}{AD}$=$\frac{CF}{DE}$=$\frac{2}{4}$=$\frac{1}{2}$.
点评 本题考查了平行四边形的判定和性质以及平行四边形的面积公式.特别是(3)注意利用平行四边形的面积公式列出等积式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.将抛物线y=2x2的图象先向上平移3个单位,再向右平移4个单位所得的解析式为( )
| A. | y=2(x-3)2+4 | B. | y=2(x+4)2+3 | C. | y=2(x-4)2+3 | D. | y=2(x-4)2-3 |
10.已知y-1与x成正比,当x=2时,y=9;那么当y=-15时,x的值为( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |

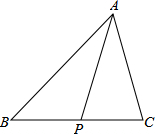 如图,在△ABC中,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点P为BC的中点,则$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示)
如图,在△ABC中,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点P为BC的中点,则$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示) 如图,点E是平行四边形ABCD的对角线AC上任意一点,求证:S△BEC=S△CDE.(两种证法)
如图,点E是平行四边形ABCD的对角线AC上任意一点,求证:S△BEC=S△CDE.(两种证法)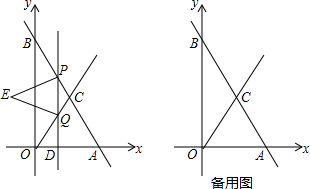
 如图,AB⊥CD于O,直线EF经过点O,OG⊥EF,∠COG=2∠BOE,求∠BOE,∠AOF,∠AOE的度数.
如图,AB⊥CD于O,直线EF经过点O,OG⊥EF,∠COG=2∠BOE,求∠BOE,∠AOF,∠AOE的度数.