题目内容
10. 如图,在正六边形ABCDEF中,连接AE,DF,则∠1=120°.
如图,在正六边形ABCDEF中,连接AE,DF,则∠1=120°.
分析 由正六边形的性质得出∠AFB=∠DEF=120°,AF=EF=DE,由等腰三角形的性质和三角形内角和定理得出∠FAE=∠FEA=∠EFD=30°,求出∠AFD=90°,由三角形的外角性质即可求出∠1的度数.
解答 解:∵六边形ABCDEF是正六边形,
∴∠AFB=∠DEF=120°,AF=EF=DE,
∴∠FAE=∠FEA=∠EFD=(180°-120°)÷2=30°,
∴∠AFD=120°-30°=90°,
∴∠1=∠FAE+∠AFD=30°+90°=120°.
故答案为:120.
点评 本题考查了正六边形的性质、等腰三角形的性质、三角形内角和定理、三角形的外角性质;熟练掌握正六边形的性质,求出∠FAE和∠AFD是解决问题的关键.

练习册系列答案
相关题目
11.解不等式组$\left\{\begin{array}{l}{2-x≤2(x+4)}\\{x<\frac{x-1}{3}+1}\end{array}\right.$,并写出该不等式组的最大整数解.
15.已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 3cm或6cm |
20.某商场利用摸奖开展促销活动,中奖率为$\frac{1}{3}$,则下列说法正确的是( )
| A. | 若摸奖三次,则至少中奖一次 | |
| B. | 若连续摸奖两次,则不会都中奖 | |
| C. | 若只摸奖一次,则也有可能中奖 | |
| D. | 若连续摸奖两次都不中奖,则第三次一定中奖 |
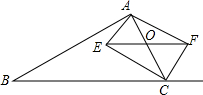 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.