题目内容
2．已知a是一元二次方程x2+3x-2=0的实数根，求代数式$\frac{a-3}{{{a^2}-2a}}÷（{a+2-\frac{5}{a-2}}）$的值．分析 先算括号里面的，再算除法，由a是方程x2+3x-2=0的实数根得出a2+3a=2，代入代数式进行计算即可．
解答 解：原式=$\frac{a-3}{a（a-2）}$÷[$\frac{（a+2）（a-2）}{a-2}$-$\frac{5}{a-2}$]
=$\frac{a-3}{a（a-2）}$÷$\frac{{a}^{2}-9}{a-2}$
=$\frac{a-3}{a（a-2）}$•$\frac{a-2}{（a+3）（a-3）}$
=$\frac{1}{a（a+3）}$
=$\frac{1}{{a}^{2}+3a}$，
∵a是方程x2+3x-2=0的实数根，
∴a2+3a=2
∴原式=$\frac{1}{a（a+3）}$=$\frac{1}{{a}^{2}+3a}$=$\frac{1}{2}$．
点评 本题考查的是分式的化简求值，此类题型的特点是：利用方程解的定义找到相等关系，再把所求的代数式化简后整理出所找到的相等关系的形式，再把此相等关系整体代入所求代数式，即可求出代数式的值．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，在正六边形ABCDEF中，连接AE，DF，则∠1=120°．
17．下列说法中正确的是（ ）
| A． | “明天降雨的概率为$\frac{1}{2}$”，表示明天有半天都在降雨 | |
| B． | “抛一枚硬币，正面朝上的概率为$\frac{1}{2}$”，表示每抛两次就有一次正面朝上 | |
| C． | “抛一枚均匀的正方体骰子，朝上的点数是6的概率为$\frac{1}{6}$”，表示随着抛掷次数的增加，“抛出朝上的点数是6”这一事件发生的概率稳定在$\frac{1}{6}$附近 | |
| D． | 某种彩票的中奖概率为$\frac{1}{1000}$，说明每买1000张，一定有一张中奖 |
如图，有一块三角形材料（△ABC），请用尺规画出△ABC的外接圆．（不写作法，保留作图痕迹）
11．在某次试验数据整理过程中，某个事件发生的频率情况如下表所示．
估计这个事件发生的概率是0.25（精确到0.01），试举出一个随机事件的例子，使它发生的概率与上述事件发生的概率大致相同：从红桃A、黑桃A、梅花A、方块A四张牌中，随机抽取一张，则抽到方块A的概率为0.25．
| 试验次数 | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 事件发生的频率 | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |
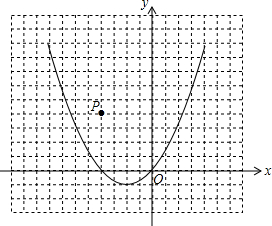已知二次函数y=x2+x的图象，如图所示