题目内容
11.解不等式组$\left\{\begin{array}{l}{2-x≤2(x+4)}\\{x<\frac{x-1}{3}+1}\end{array}\right.$,并写出该不等式组的最大整数解.分析 先解不等式①,去括号,移项,系数化为1,再解不等式②,取分母,移项,然后找出不等式组的解集.
解答 解:$\left\{\begin{array}{l}{2-x≤2(x+4)①}\\{x<\frac{x-1}{3}+1②}\end{array}\right.$
解不等式①得,x≥-2,
解不等式②得,x<1,
∴不等式组的解集为-2≤x<1.
∴不等式组的最大整数解为:-2,-1,0,
点评 此题是一元一次不等式组的整数解题,主要考查了不等式得解法和不等式组的解集的确定及整数解的确定,解本题的关键是不等式的解法运用.

练习册系列答案
相关题目
2.下列图案中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )| A. | 34° | B. | 54° | C. | 66° | D. | 56° |
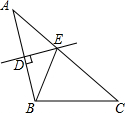 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为13.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为13. 如图,在正六边形ABCDEF中,连接AE,DF,则∠1=120°.
如图,在正六边形ABCDEF中,连接AE,DF,则∠1=120°.