题目内容
1.如图,在平面直角坐标系中,己知点A(3,0),点B(0,4),第1次将△ABO绕点A顺时针旋转到△AP1M1的位置,点B,O分别落在点P1,M1处,点P1在x轴上;第2次将△AP1M1绕点P1顺时针旋转到△M2P1P2的位置,点M1、A分期落在点P2、M2处,点P2在x轴上;第3次将△M2P1P2绕点P2顺时针旋转到△P3M3P2的位置,点M2、P1分期落在点P3、M3处,点P3在x轴上;…依次进行下去,直至得到△M2015P2014P2015为止,点P2015在x轴上,则点P2015的坐标为(8064,0).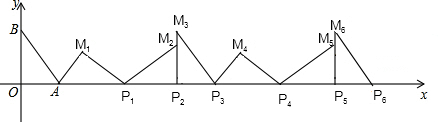
分析 首先利用勾股定理得出AB的长,进而得出三角形的周长,进而求出p2,p5的横坐标,进而得出变化规律,即可得出答案.
解答 解:由题意可得:∵AO=3,BO=4,
∴AB=5,
∴OA+Ap1+p1p2=3+5+4=12,
∴P2的横坐标为:12=(2+1)÷3×12,P5的横坐标为:2×12=24=(5+1)÷3×12,
∵(2015+1)÷3=672
∴OP2015=672×12=8064
故P2105的坐标为(8064,0).
故答案为(8064,0).
点评 此题主要考查了点的坐标以及图形变化类,根据题意得出P点横坐标变化规律是解题关键.

练习册系列答案
相关题目
9. 星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )
星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )
 星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )
星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )| A. | 小王去时的速度大于回家的速度 | |
| B. | 小王在朋友家停留了10分钟 | |
| C. | 小王去时花的时间少于回家时所花的时间 | |
| D. | 小王去时走下坡路,回家时走上坡路 |
6.下列等式中正确的是( )
| A. | a3•(-3a2)=-3a6 | B. | 6(b-a)2-2(a-b)=2(a-b)(3a-3b-1) | ||
| C. | (-2a-3b)(2a-3b)=4a2-9b2 | D. | (-a)6÷(-a)3=a2 |
13.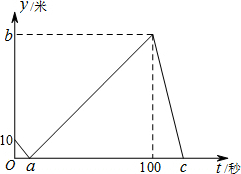 甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
 甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )| A. | 仅有①② | B. | 仅有② | C. | 仅有②③ | D. | ①②③ |
10.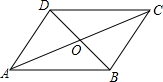 如图,在?ABCD中,AD=5,AC=10,BD=6,则△BOC的周长为( )
如图,在?ABCD中,AD=5,AC=10,BD=6,则△BOC的周长为( )
 如图,在?ABCD中,AD=5,AC=10,BD=6,则△BOC的周长为( )
如图,在?ABCD中,AD=5,AC=10,BD=6,则△BOC的周长为( )| A. | 13 | B. | 16 | C. | 18 | D. | 21 |
11.若关于x的不等式mx-n>0的解集是x<$\frac{1}{4}$,则关于x的不等式(n-m)x>(m+n)的解集是( )
| A. | x<-$\frac{5}{3}$ | B. | x>-$\frac{5}{3}$ | C. | x<$\frac{5}{3}$ | D. | x>$\frac{5}{3}$ |
 如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).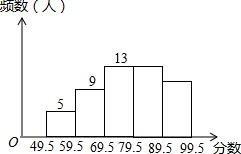 某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.
某中学八年级共有400名学生,学校为了增强学生的国防意识,在本年级进行了一次国防知识测验.为了了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.