题目内容
12. 如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
分析 先利用两点间的距离公式计算出AD=2,再根据菱形的性质得到CD=AD=2,CD∥AB,然后根据平行于x轴的直线上的坐标特征写出C点坐标.
解答 解:∵点D的坐标为(1,$\sqrt{3}$),
∴AD=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵四边形ABCD为菱形,
∴CD=AD=2,CD∥AB,
∴C点坐标为(3,$\sqrt{3}$).
故答案为(3,$\sqrt{3}$).
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了坐标与图形性质.

练习册系列答案
相关题目
2.为了了解某校学生的课外阅读情况,随机抽查了10学生周阅读用时数,结果如下表:
则关于这10名学生周阅读所用时间,下列说法正确的是( )
| 周阅读用时数(小时) | 4 | 5 | 8 | 12 |
| 学生人数(人) | 3 | 4 | 2 | 1 |
| A. | 中位数是6.5 | B. | 众数是12 | C. | 平均数是3.9 | D. | 方差是6 |
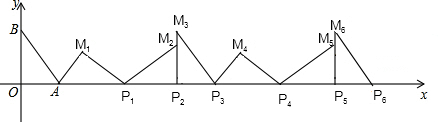
7. 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
17.已知样本容量为30,样本频数分布直方图中各小长方形的高的比依次是2:4:3:1,则第二小组的频数是( )
| A. | 14 | B. | 12 | C. | 9 | D. | 8 |
4.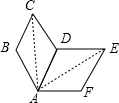 如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
 如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )
如图,四边形ABCD经过旋转后与ADEF重合,则下面各角不是旋转角的是( )| A. | ∠BAD | B. | ∠CAE | C. | ∠DAF | D. | ∠CAF |
2.平安集团在深圳福田CBD修建的平安大厦是深圳新的地标建筑,该地于2007年11月6日以16.568亿元拍得.这个数据用科学记数法表示是( )
| A. | 16.568×108元 | B. | 1.6568×108元 | C. | 1.6568×109元 | D. | 16.568×109元 |