题目内容
8.△ABC中,AB=10,AC=17,BC边上的高AD=8,则线段BC的长为9或21.分析 由勾股定理可分别在Rt△ABD和Rt△ADC中求出BD、DC的长,然后分两种情况考虑:①D点在线段BC上,②D点在CB的延长线上;根据D点的不同位置可得BD、DC、BC三条线段不同的数量关系,从而得到BC的值.
解答  解:Rt△ACD中,AC=17,AD=8,
解:Rt△ACD中,AC=17,AD=8,
由勾股定理得:CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=15;
Rt△ABD中,AB=10,AD=8,由勾股定理得:BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=6;
①点D在线段BC上时,BC=BD+CD=21,
②点D在CB的延长线上时,BC=CD-BD=9,
故BC的长为9或21.
故答案为:9或21.
点评 此题主要考查的是勾股定理的应用,应注意的是点D的位置有两种情况,要分类讨论,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.不等式3x≤x+m的正整数解只有2个,则m的取值范围是( )
| A. | 4<m<6 | B. | 4≤m≤6 | C. | 4≤m<6 | D. | 4<m≤6 |
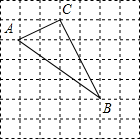 △ABC在如图所示的方格中,正方形小方格边长为1
△ABC在如图所示的方格中,正方形小方格边长为1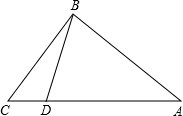 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t=$\frac{5}{2}$或3或3.6时,△CBD是等腰三角形.
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t=$\frac{5}{2}$或3或3.6时,△CBD是等腰三角形. 如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm.
如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm.