题目内容
13.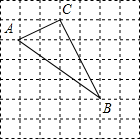 △ABC在如图所示的方格中,正方形小方格边长为1
△ABC在如图所示的方格中,正方形小方格边长为1(1)在图中方格中画出以A、B、C为顶点的平行四边形;
(2)所画平行四边形的面积为10,△ABC边AB上的高为2.
分析 (1)根据两组对边平行分别平行的四边形是平行四边形画出图形即可;
(2)首先利用勾股定理计算出AC、BC、AB的长,然后再利用勾股定理逆定理证出∠ACB是直角,进而可得算出平行四边形的面积;再根据直角三角形的面积公式计算出AB上的高即可.
解答 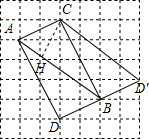 解:(1)如图所示:
解:(1)如图所示:
(2)AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵($\sqrt{5}$)2+(2$\sqrt{5}$)2=52,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴面积为:$\sqrt{5}$×2$\sqrt{5}$=10.
过C作CH⊥AB,
∵S△ACB=$\frac{1}{2}×$AC•CB=$\frac{1}{2}$AB•CH,
∴$\sqrt{5}$×2$\sqrt{5}$=5×AH,
AH=2.
故答案为:10;2.
点评 此题主要考查了平行四边形的判定,以及勾股定理和逆定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在$\sqrt{3}$,-1,0,-$\sqrt{2}$这四个数中,最大的是( )
| A. | $\sqrt{3}$ | B. | 0 | C. | -1 | D. | -$\sqrt{2}$ |
12.已知∠AOB=65°,∠BOC=15°,则∠AOC等于( )
| A. | 80° | B. | 40° | C. | 80°或40° | D. | 以上都不对 |
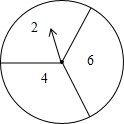 把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.
把一个转盘平均分成三等份,依次标上数字2、4、6,小红自由转动转盘两次,把第一次转动停止后指针指向的数字记作x,把第二次转动停止后指针指向的数字除以2所得的商记作y,以x,y,5的边长的三条线段,能够构成三角形的概率为$\frac{4}{9}$.